数学A(平面図形):チェバの定理 対象 高1 再生時間 441 説明文・要約 ・三角形の内部に頂点から3本の線を引いたとき、3組の辺の比をかけたら必ず「1」になる ・ メネラウスの定理 と異なり、三角形の三辺上をたどっていく (全体的に チェバの定理は,線分の長さや線分の比を求めるために使われることが多いです。 例題 A F F B = 1 2 AFFB=12 A F FB = 1 2教科書・プリント・問題集 11月図形の性質 ①三角形の性質 三角形と比、中点連結定理、内分・外分、内閣の二等分線と比、外角の二等分線と比、メネラウスの定 理、チェバの定理 教科書・プリント・問題集 2月図形の性質 (1月の引き続き) ③作図
チェバの定理とメネラウスの定理をてんびん算と連比で解く 父ちゃんが教えたるっ
チェバの定理 問題集
チェバの定理 問題集- 教科書 数A 啓林館, 単元 三角形の性質, 「チェバ・メネラウスの定理を覚えられない、理解できないそこの貴方! 曖昧な理解で済ませがちなこの定理を"感覚で"覚えられるようにノートを作成しました! 初めてのノート投稿となりますが、ぜひ🖤マークをよろしくお願いします。」, 学年 チェバの定理の証明などは、こちらの記事をどうぞにゃん 『数学「チェバの定理」とは?定理の覚え方や問題(例題)、証明、面積比との関係などをまとめました。チェバの定理の逆もどうぞ平面図形 中学数学 高校数学』




チェバの定理とは その覚え方と証明を解説 演習問題つき Himokuri
チェバの定理は各頂点と各分点 (辺の途中にある点)を、頂点→分点→頂点→・・・と進み、 一周すれば、長さの関係式を穴埋めすることができます。 覚え方としては三角形をチェバの定理は、三角形の頂点から分点へ辺を順番になぞっていくイメージです。5分で解ける! チェバの定理2応用に関する問題 映像授業 Try IT(トライイット) 575K subscribers Subscribe 高校 数学A 図形18 チェバの定理2 (10分) Info Shoppingチェバの定理まずは簡単な方、「チェバの定理」です。 この定理(式)の覚え方はとても簡単です。 三角形の頂点を (白丸)、辺上の点を (黒丸)とすれば、どこでもいいので、スタート地点を決めて、時計回りでも反時計回りでもいいので、ぐるりと \(1\) 周します。
チェバの定理の逆 abcの辺bc, ca, abまたはその延長上にそれぞれ点p,q,rがあり、この3点のうち辺の延長上にあるのは0または2個だとする。 このとき bqとcrが交わり、かつ bp pc ・ cq qa ・ ar rb =1 が成り立つなら3直線ap, bq, crは1点で交わる。 a b c p q r メネラウスの 1 数学「チェバの定理」とは? 定理の覚え方や問題(例題)、証明、面積比との関係などをまとめました。 チェバの定理の逆もどうぞ平面図形 中学数学 高校数学 11 チェバの定理が使える図形とは 12 チェバの定理とは? 13 チェバの定理の覚え方 14 チェバの定理を使う問題(例題) 15 チェバの定理と面積比 16 チェバの定理の証明 メネラウスの定理とチェバの定理 「 メネラウスの定理 」と「 チェバの定理 」は聞いたことがある方も多いのではないでしょうか。 高校受験ではとても役に立つ公式です。 知らなくても補助線を引いたりして、計算をすれば同じ答えに辿り着けますが、知っていると簡単に答えが出る問題が多くあります。 「メネラウスの定理」と「チェバの定理」が
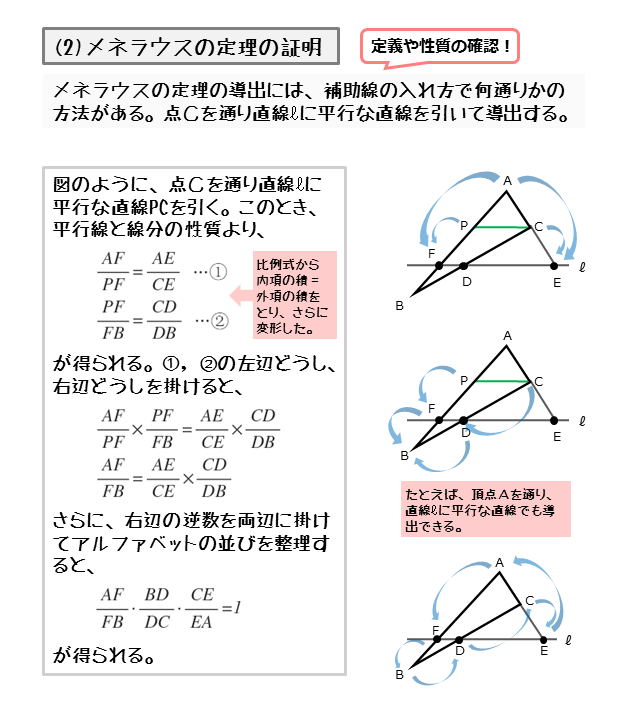
(注)方べきの定理は逆も成り立つ。 ※ 2つの円の位置関係、共通接線についても確認しておく。 下図のように ABCにおいて、辺BC,CA,AB上またはその延長 上にそれぞれP,Q,Rがあり、AP,BQ,CRが1点Oで交わると き (7)チェバの定理 qa cq pc bp rb ar × =1空間におけるチェバの定理の類似について 21年6月 片山 喜美 n君から、21年前期大阪大学入試問題 第2問について「ベクトルでは無く幾何で はどのように解きますか?」という質問をもらった。普通にはベクトルの問題で、幾何で 問題2(1) 「台形の証明」という実は見慣れないものなので,どうやって書いたらよいか分からない中学生多そう。 何なら平行四辺形の定理定義は知っていても,台形の成り立つ条件は意外と知らない中学生多そう。 知っていれば楽勝の問題です。 問題2(2)



この問題に チェバの定理 メネラウスの定理 どちらを用いればい Yahoo 知恵袋




チェバの定理 おいしい数学
「チェバの定理の逆」に関する問題と数 学の考え方について いきなりですが、チェバの定理を使って解く有名問題と、その解答を掲載します。なぜ、 そのような解答にいたったか?ということは、解答の後に記載していくことにします。 なお、チェバの定理やメネラウスの定理では、その覚え方にコツがあります。 どちらの定理でも、 スタートした頂点に必ず戻ってくる ように、また アルファベットがつながる ように式を作ることができます。 噂では正答率が0%らしい空間図形の問題を紹介します。 時間足りなかったら解けません。 時間あっても解けないんじゃないか? (体積じゃなくて比率にすればよかったのに,(2)②) 配点が福島県は高校によって変わるらしいので,PDFの配点




チェバ メネラウスの定理の問題です 解き方と答え教えてください Clearnote




チェバの定理の逆による証明ですが チェバの定理が成り立つと仮定してから結果的 Clearnote
チェバ・メネラウスの定理の逆 三角形の各頂点から引いた3本の線が1点で交わることを証明する問題、あるいは、3点が1直線上にあることを証明する問題。 利用します。 ということです。 このように、図形に関する定理は逆が成り立つことを知っておきプリント教材 数学Ⅰ・A 挑戦してみたい因数分解・問題 対称式 2次関数のグラフ 線分の和の最小値問題 チェバの定理・証明問題 チェバの定理の逆・証明問題 その2 1301(メネラウスの定理) 1302(チェバの定理) 1303(中線定理) 1304(角の二等分線の定理) 1310(辺の長さの比と三角形の面積の比) 1311(三角形の面積の公式リスト(ヘロンの公式も含む)) 1343(方べきの定理・接弦定理) 1350(四角形の分類) ・14章(初等幾何(空間)) 1400(直円錐の側面積)




数学 面積比と線分比をシッカリわかると チェバの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生




3講 チェバ メネラウス の定理 1節 平面図形 問題集 2章 図形の性質
5 メネラウスの定理やチェバの定理を扱った問題を解いてみよう 51 問1の解答・解説;メネラウスの定理② メネラウスの定理③ チェバの定理① チェバの定理② チェバの定理③ チャート(まとめ集全6枚(a4普通紙) 価格800円(税込) 数学a 平面幾何 試験によく出る相似形 センター試験の平面幾何では、かなりの頻度で相似の問題が出題されます。3講 チェバ・メネラウス の定理(1節 平面図形) 問題集2章 図形の性質です。わかりやすいポイントと例題つきの問題集です!定期テスト対策にお使いください。全て無料でダウンロードできます。塾や家庭教師、学校でご自由にお使いください!



1



図形の性質 メネラウスの定理 チェバの定理について 日々是鍛錬 ひびこれたんれん
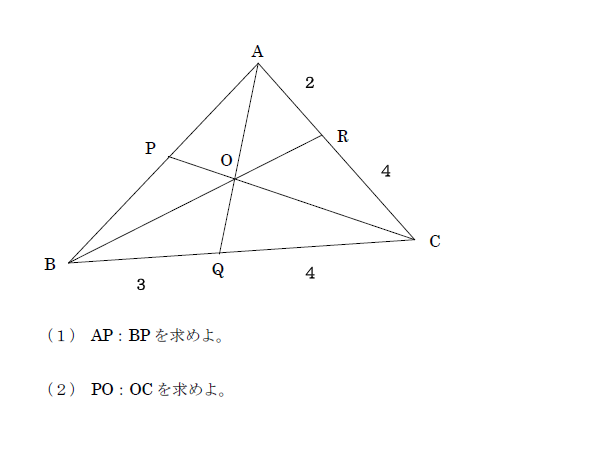
数学・算数 問題. ABCの辺AB、AC上にそれぞれ点D、Eを AD:DB=t:1、 AE:EC=1:(t+1) となるようにとる。さらにBEとCDの交点をPとし、PとAを結ぶ直線がBCと交わる チェバ・メネラウスの定理は、どちらも同じような式になっています。 よくある間違いは、分母と分子を書き間違えることです。 普段は分母から書いているのを分子から書くことが多いので間違えることになるのです。 機械的に埋められるようになれば、間違いは減ります。 問題演習を積み重ねれば良いだけのことです。 問題集が全部解けるようにする 体系数学を使っている学校の場 1 1 回答 チェバの定理とメネラウスの定理の難しい問題を教えてください。 チェバの定理とメネラウスの定理の難しい問題を教えてください。 問題集を一通り解き終って意外にも簡単だったので難しい問題をやってみたいです。 本屋に寄ってみたのですがどれも同じだったので探しています。 回答で問題を出してもいいですからお願いします。 あと




高校数学a メネラウスの定理2 応用 例題編 映像授業のtry It トライイット



1
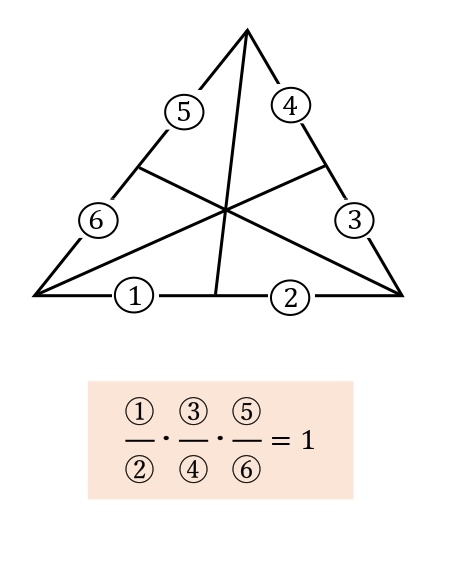
数学の分野で嫌いな人が多いと思われるメネラウス・チェバの定理に関する裏技です。 この解法はかなり使えます! まずは問題を見てください。 ↓ このような問題は通常メネチェバの公式を使って解きますが、てんびんあるいはシーソーの考えを利用高校入試で役立つ公式・定理 平面図形編 ・この公式集について 公式・定理などとうたってはいますが、その導出過程にある考え方は問題 16 チェバの定理 c af fb 問題編チェバの定理 チェバの定理 ABCの点A、B、Cと点Oを結ぶ各直線が対辺あるいは延長上と交わる点をP、Q、Rとしたとき、次の式が成り立ちます。 チェバの定理 ※点Oは三角形の辺上や延長線上にはないものとします。 チェバの定理の覚え方 よくあるチェバの定理の覚え方として、下の図のように三角形を左回りに見て、分数の式をつくる方法があります。 ①②、③④、⑤⑥



高校数学a 図形の性質 公式一覧 チェバ メネラウス 接弦 方べき 学校よりわかりやすいサイト




3講 チェバ メネラウス の定理 1節 平面図形 問題集 2章 図形の性質
このチェバの定理・・・昭和時代中学生だった私たち夫婦は習っていません。 ネットで見ると、平面幾何は、この方法を使うと、簡単らしいですが、 もともと幾何が苦手な私は、ちんぷんかんぷん。 わが子が得意げに言うので、問題集の問題を、方べきの定理で求める 年 (令和2年)度に行われたセンター試験数学1Aの選択問題の1つ第5問平面幾何の解説です。 平面幾何(図形)で問われる定理はおおよそ限られているので基本的な定理をしっかり覚えていればそれほど得点しにくい分野ではありません。 今回はチェバ、メネラウス、方べきの定理が主な問題となります。 センター試験年度数学 ⅠA の問題 ここでは AMNと ABCが相似であることの証明を利用する方法を考えます。 AMNと ABCにおいて M,Nが辺AB、辺ACの中点なので AMAB=12 ‥① ANAC=12 ‥② ∠MAN=∠BAC(共通な角)‥③ ①、②、③より AMN∽ ABC 相似比は12なので MNBC=12 よってMN=1/2BC また 相似な図形の対応する角なので ∠AMN=∠ABC




高校数学a チェバの定理1 基本 練習編 映像授業のtry It トライイット



受験 定期試験 数学解き方集 裏技 解法 メネラウス チェバの定理 中学 高校




Dショッピング irisunaの定理 メネラウスの定理 チェバの定理を含む定理 前編 入砂七五三一 カテゴリ の販売できる商品 Honyaclub Com ドコモの通販サイト



某中学過去問より 回答はありますが 解法は載ってません 子供に教 Yahoo 知恵袋



数学a チェバの定理の使い方とコツ 教科書より詳しい高校数学




第3章 図形の性質 高校数学a Part2 チェバの定理 メネラウスの定理 第3章 図形の性質 脳科学式超記憶で身に付ける問題集 脳tec




チェバの定理は 三角形の内部にある点xと3頂点を結んだ直線が 3辺と交わる時 Clearnote




第3章 図形の性質 高校数学a Part2 チェバの定理 メネラウスの定理 第3章 図形の性質 脳科学式超記憶で身に付ける問題集 脳tec




チェバの定理の例題なんですけど この部分の計算の仕方がわかりません Clearnote



こんにちは 数学aのチェバの定理 メネラウスの定理系の質問です Yahoo 知恵袋




改訂版 4step数学a P130 補 チェバの定理の逆 メネラウスの定理の逆
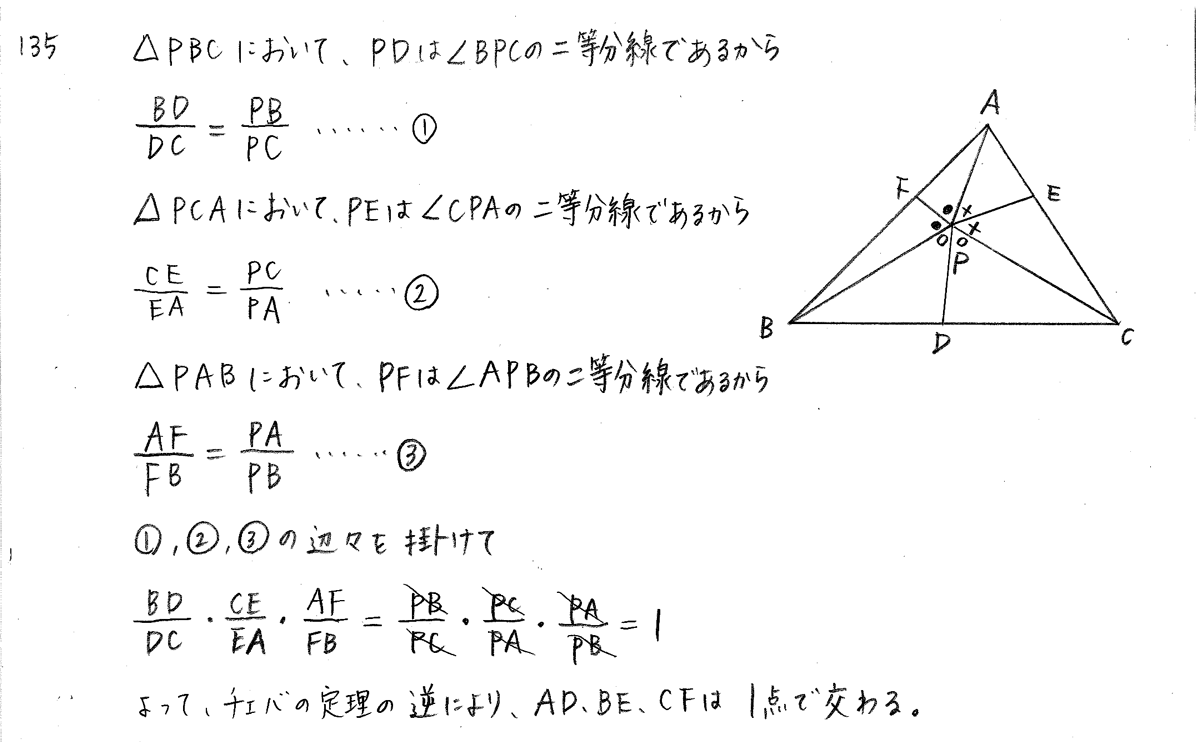



クリアー数学a 数a P121 補 チェバの定理の逆 メネラウスの定理の逆




箱ひげ図 チェバの定理とメネラウスの定理 あなたは解けますか 1冊でしっかりわかる と大人気のベストセラーシリーズに 待望の高校数学が登場 かんき出版のプレスリリース
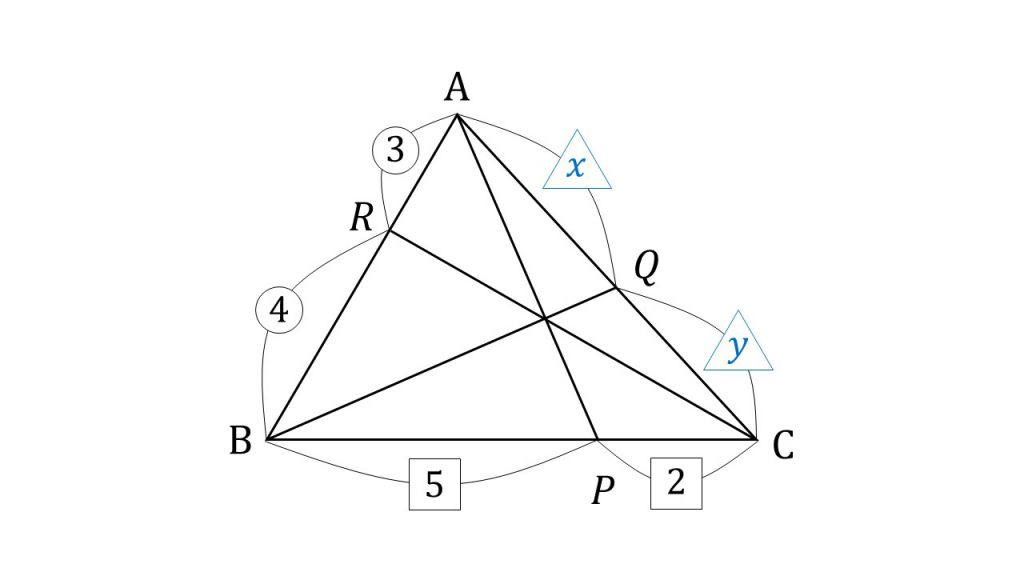



チェバ メネラウスの定理の簡単な使い方 大学受験の王道
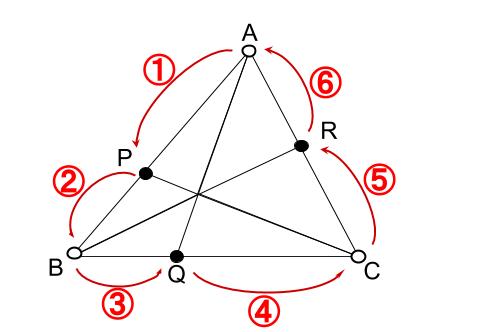



メネラウスの定理 チェバの定理 徹底解剖 高校数学の無料オンライン学習サイトko Su
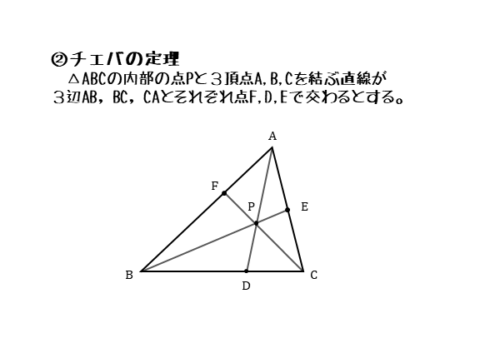



図形の性質 メネラウスの定理 チェバの定理について 日々是鍛錬 ひびこれたんれん




高校数学a 三角形の五心 三角形の重心とその存在証明 受験の月



チェバの定理とメネラウスの定理をてんびん算と連比で解く 父ちゃんが教えたるっ




チェバ メネラウスの定理が分かるようになる 個人指導シグマ 中高一貫 国立生専門塾




チェバの定理の逆 定理の仮定の利用方法がわかりません Abcの辺b Okwave




チェバの定理の275 276の解き方と解説をお願いします Clearnote




高校数学a メネラウスの定理とその逆の証明 受験の月




図形の性質 メネラウスの定理 チェバの定理について 日々是鍛錬 ひびこれたんれん




メネラウスの定理まとめ 証明 覚え方 逆 問題 理系ラボ




チェバの定理まとめ 証明 覚え方 逆 問題 理系ラボ



高校一年の数学a チェバの定理 メネラウスの定理 についての問題 Yahoo 知恵袋




チェバの定理 おいしい数学




チェバ メネラウスの定理 数学の偏差値を上げて合格を目指す




チェバの定理まとめ 証明 覚え方 逆 問題 理系ラボ
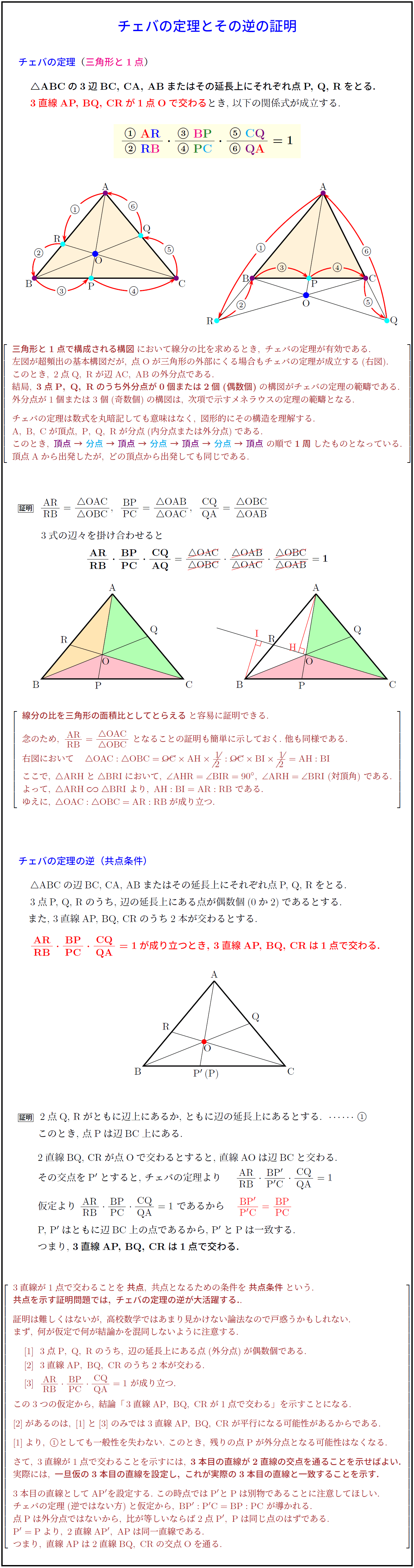



高校数学a チェバの定理とその逆の証明 受験の月



チェバの定理とメネラウスの定理をてんびん算と連比で解く 父ちゃんが教えたるっ




チェバの定理まとめ 証明 覚え方 逆 問題 理系ラボ



この図のxを求めるという問題です メネラウスの定理をつかう Yahoo 知恵袋




チェバの定理 おいしい数学



1




Tossランド チェバの定理 メネラウスの定理




チェバの定理 おいしい数学



メネラウスの定理 チェバの定理 京極一樹の数学塾




平面図形13 チェバの定理 怜悧玲瓏 高校数学を天空から俯瞰する
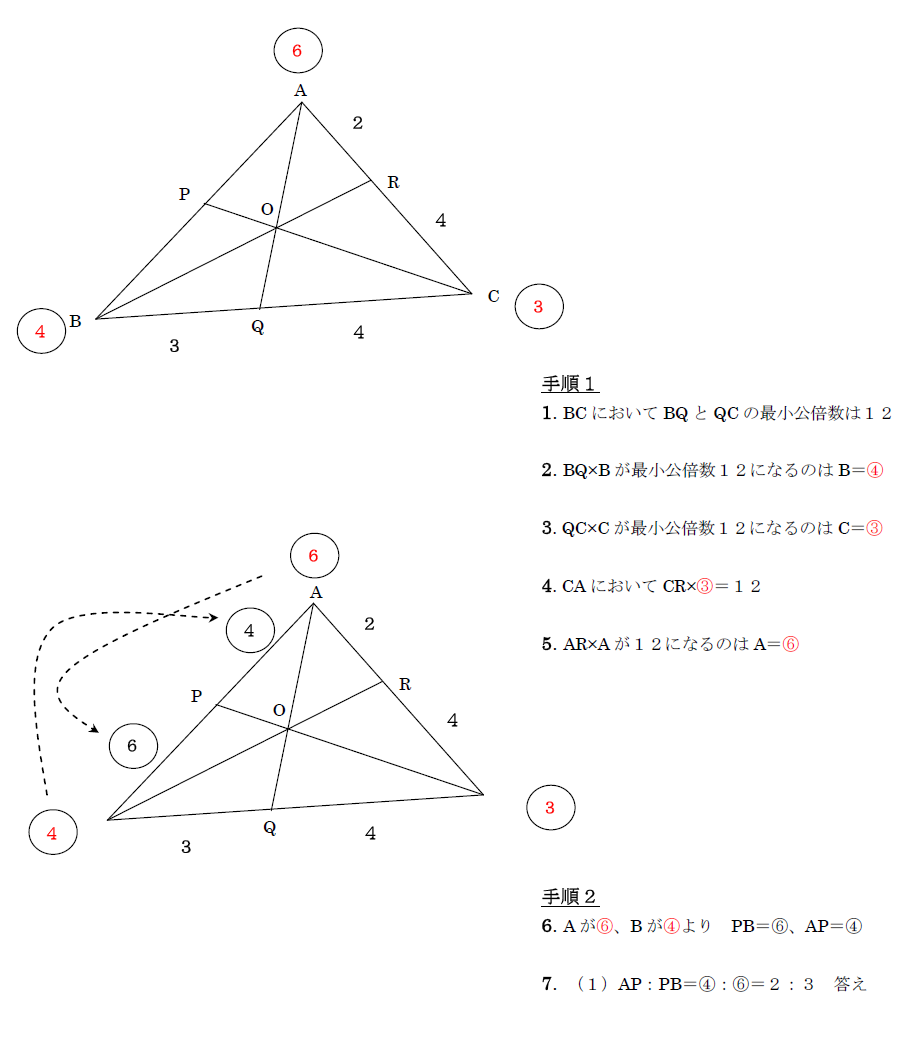



受験 定期試験 数学解き方集 裏技 解法 メネラウス チェバの定理 中学 高校



チェバの定理を使う問題 写真のような問題 で チェバの定理を使わず解こう Yahoo 知恵袋




高校数学a チェバの定理1 基本 練習編 映像授業のtry It トライイット




チェバ メネラウスの定理 数学の偏差値を上げて合格を目指す




チェバの定理 おいしい数学




数学a チェバの定理の使い方とコツ 教科書より詳しい高校数学




チェバの定理とは その覚え方と証明を解説 演習問題つき Himokuri




q a 高校数学aチェバの定理の別パターンは Youtube




メネラウスの定理 の新着タグ記事一覧 Note つくる つながる とどける
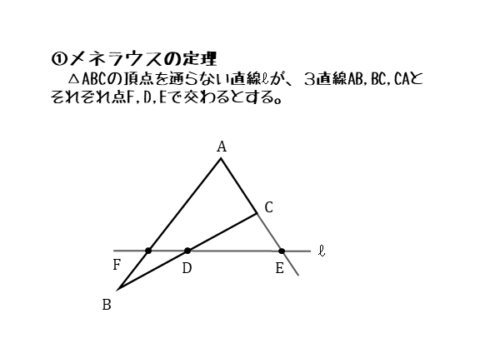



図形の性質 メネラウスの定理 チェバの定理について 日々是鍛錬 ひびこれたんれん




チェバの定理 メネラウスの定理が分からないのは 個人指導シグマ 中高一貫 国立生専門塾




チェバの定理まとめ 証明 覚え方 逆 問題 理系ラボ
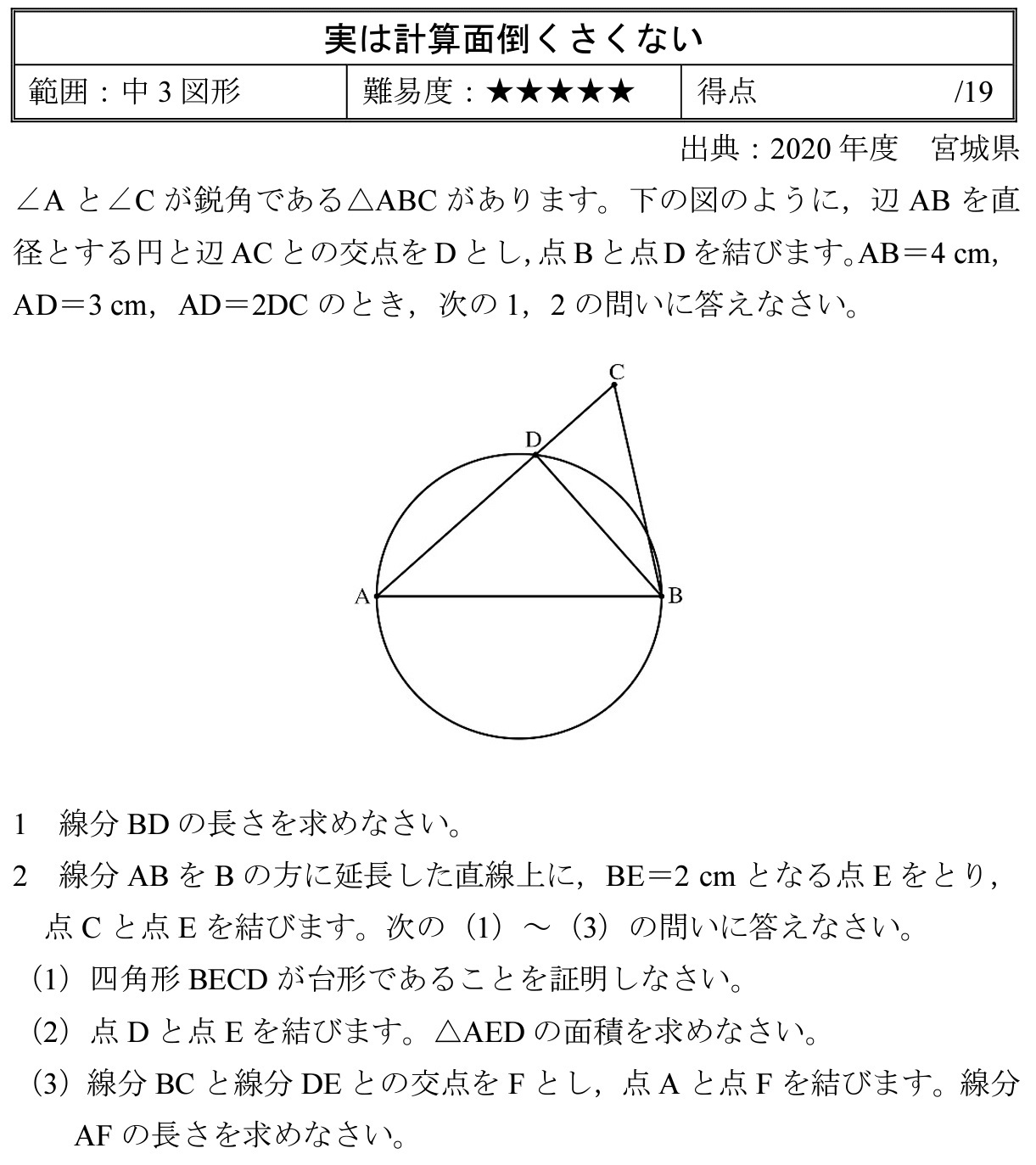



面積比難問 チェバの定理は禁止 年度宮城県 高校入試 数学 良問 難問




数学 チェバの定理 とは 定理の覚え方や問題 例題 証明 面積比との関係などをまとめました チェバの定理の逆もどうぞ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生




メネラウスの定理をベクトルで 数学の偏差値を上げて合格を目指す




数学a 平面図形 メネラウス チェバの定理 まとめ集 自宅でできる受験対策ショップ ワカルー Wakaru




チェバの定理まとめ 証明 覚え方 逆 問題 理系ラボ




メネラウスの定理やチェバの定理は 公式として覚えたらいいですか どんな問題で Clearnote




数aの問題です チェバの定理か メネラウスの定理を使って解くと思うのですが Clearnote




数学 チェバの定理 とは 定理の覚え方や問題 例題 証明 面積比との関係などをまとめました チェバの定理の逆もどうぞ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生



Tossランド チェバの定理 メネラウスの定理




チェバの定理とは その覚え方と証明を解説 演習問題つき Himokuri




改訂版 クリアー数学a P132 12 チェバの定理 メネラウスの定理




箱ひげ図 チェバの定理とメネラウスの定理 あなたは解けますか 1冊でしっかりわかる と大人気のベストセラーシリーズに 待望の高校数学が登場 かんき出版のプレスリリース
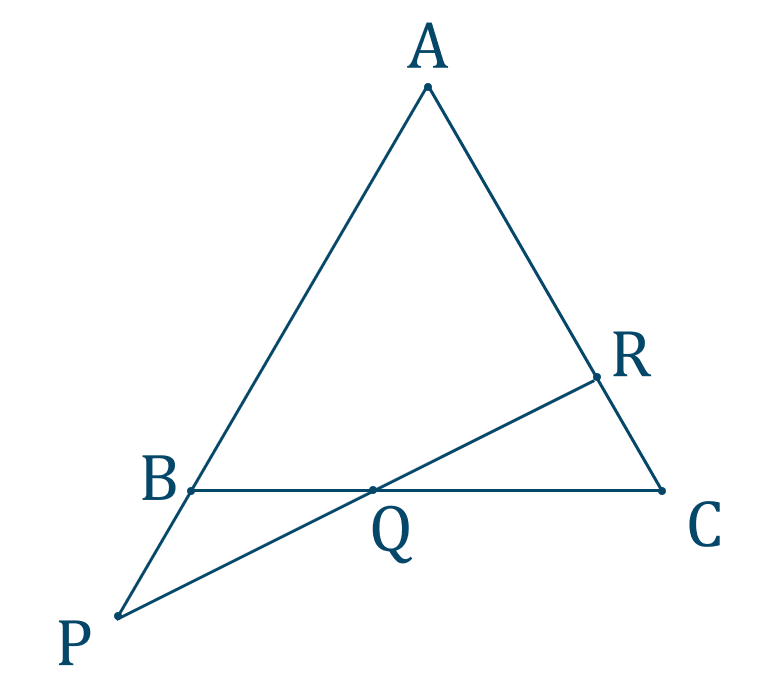



数学a メネラウスの定理の使い方とコツ 教科書より詳しい高校数学




数学 チェバの定理 とは 定理の覚え方や問題 例題 証明 面積比との関係などをまとめました チェバの定理の逆もどうぞ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生




チェバ メネラウスの定理 数学の偏差値を上げて合格を目指す




数学a 平面図形 メネラウス チェバの定理 まとめ集 自宅でできる受験対策ショップ ワカルー Wakaru



チェバ メネラウスの定理の逆 大学受験の王道




改訂版 クリアー数学a P133 補 チェバの定理の逆 メネラウスの定理の逆




改訂版 クリアー数学a P132 12 チェバの定理 メネラウスの定理




3講 チェバ メネラウス の定理 1節 平面図形 問題集 2章 図形の性質




書籍 新aクラス中学幾何問題集 6訂版 をワードクラウド化 新感クラウド
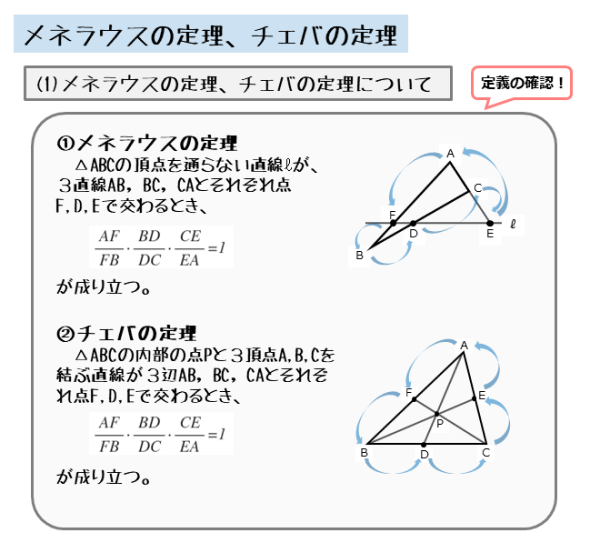



図形の性質 メネラウスの定理 チェバの定理について 日々是鍛錬 ひびこれたんれん
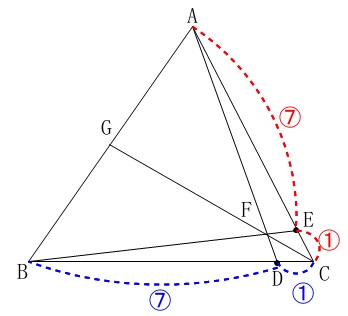



年 令和2年 度センター試験数学1a第5問の解説




改訂版 3trial数学a P121 3 チェバの定理 メネラウスの定理




高校数学a チェバの定理とメネラウスの定理の基本問題演習 受験の月
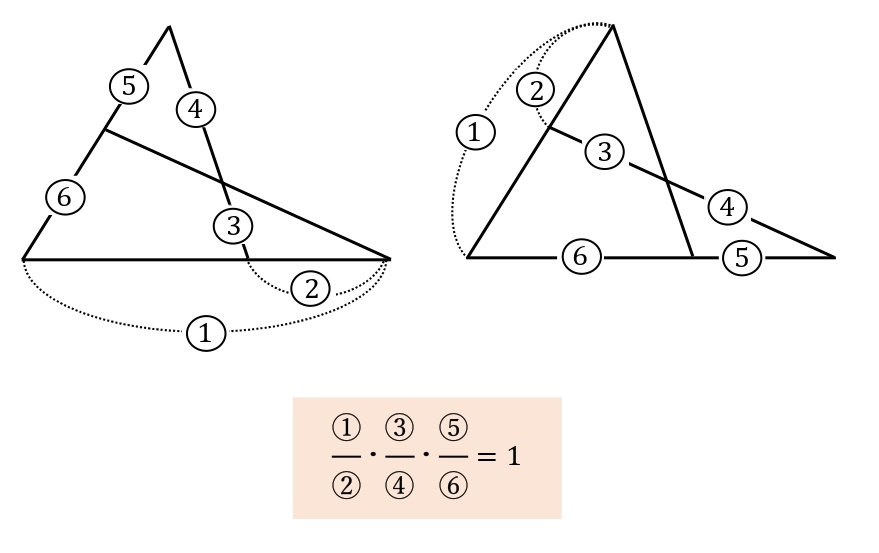



高校数学a 図形の性質 公式一覧 チェバ メネラウス 接弦 方べき 学校よりわかりやすいサイト



1




数学a 平面図形 メネラウス チェバの定理 まとめ集 自宅でできる受験対策ショップ ワカルー Wakaru




高校数学a チェバの定理1 基本 練習編 映像授業のtry It トライイット




チェバの定理 おいしい数学




チェバの定理の新着記事 アメーバブログ アメブロ
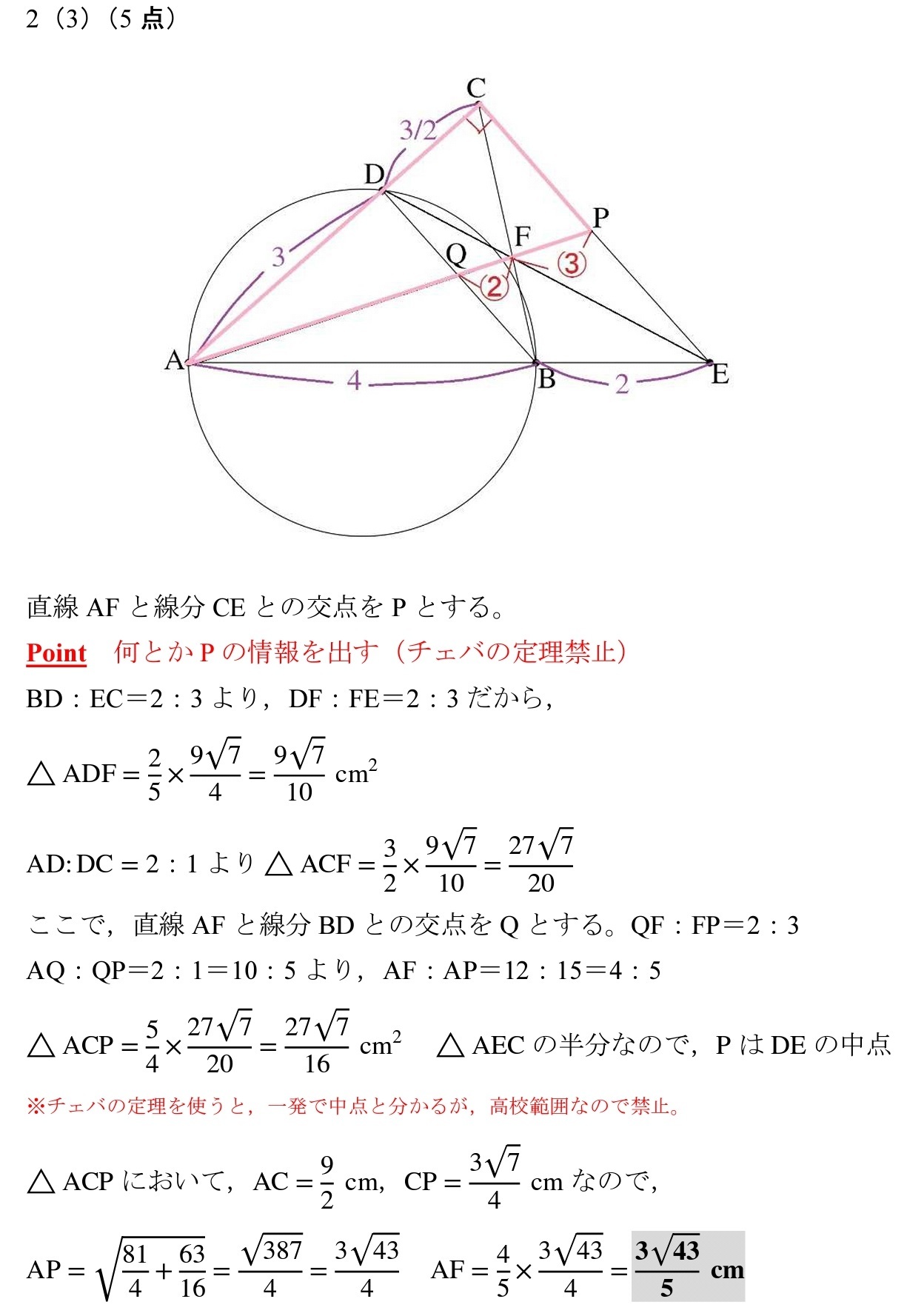



面積比難問 チェバの定理は禁止 年度宮城県 高校入試 数学 良問 難問
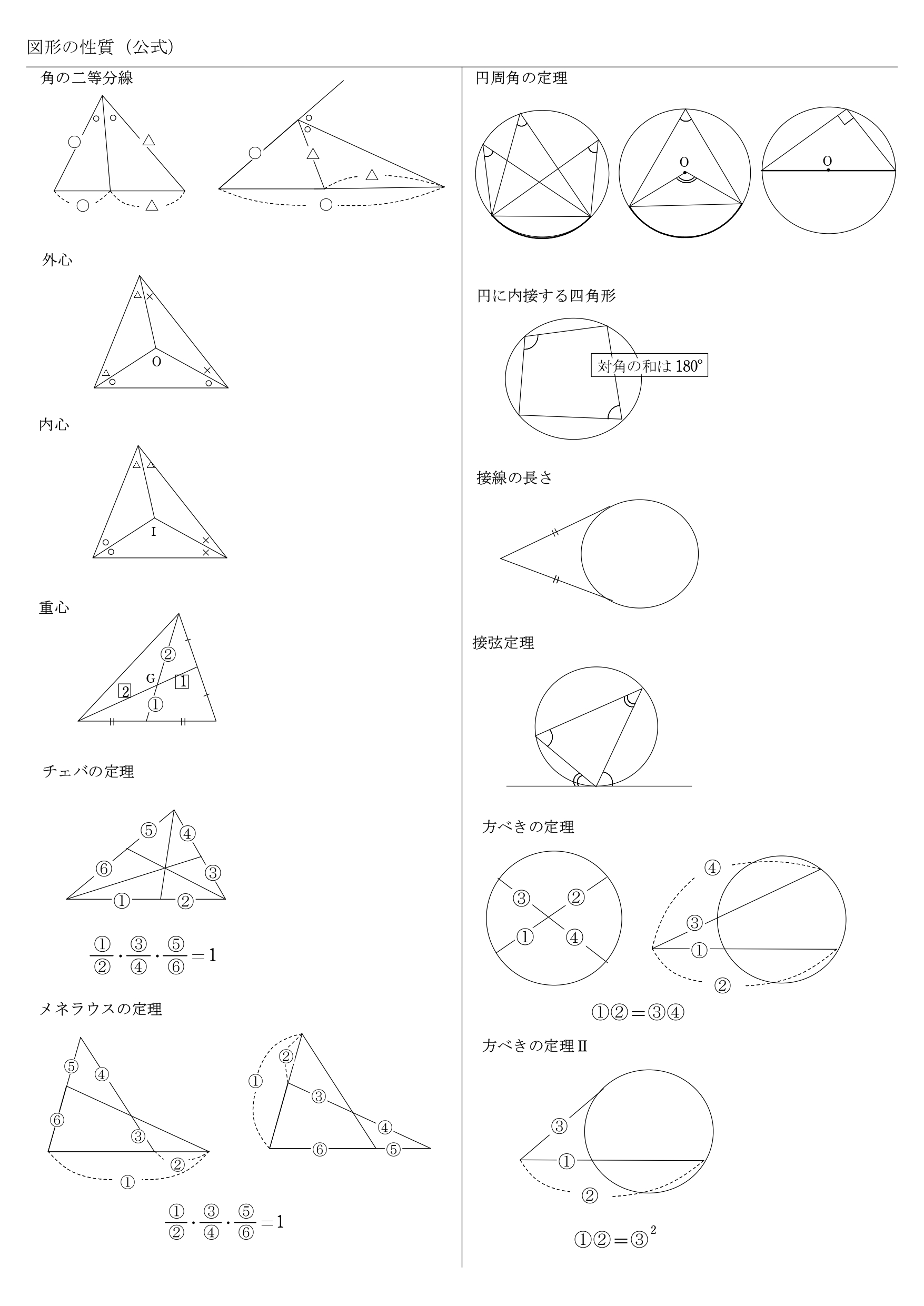



高校数学a 図形の性質 公式一覧 チェバ メネラウス 接弦 方べき 学校よりわかりやすいサイト
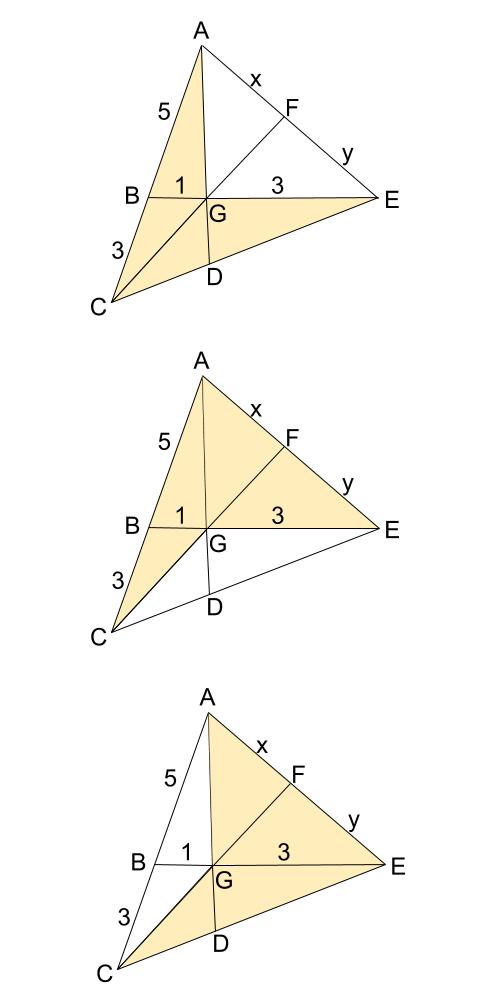



メネラウスの定理 チェバの定理 徹底解剖 高校数学の無料オンライン学習サイトko Su




チェバの定理 メネラウスの定理が分からないのは 個人指導シグマ 中高一貫 国立生専門塾




数学 チェバの定理 とは 定理の覚え方や問題 例題 証明 面積比との関係などをまとめました チェバの定理の逆もどうぞ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生




メネラウスの定理 チェバの定理 徹底解剖 高校数学の無料オンライン学習サイトko Su



チェバの定理とメネラウスの定理をてんびん算と連比で解く 父ちゃんが教えたるっ
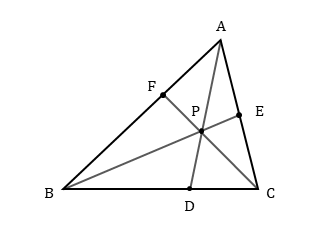



図形の性質 メネラウスの定理 チェバの定理について 日々是鍛錬 ひびこれたんれん
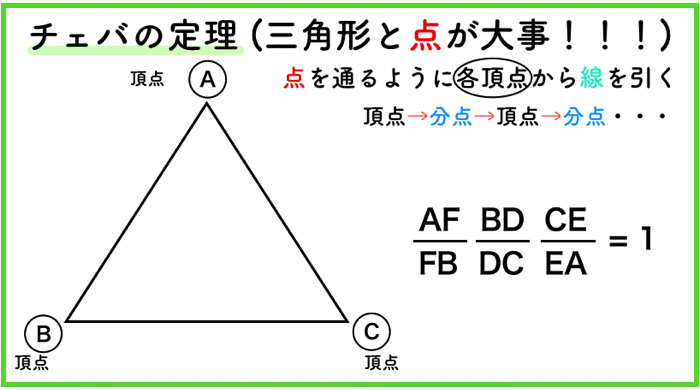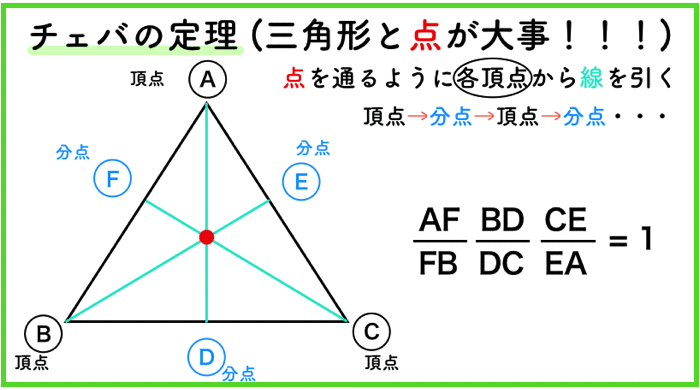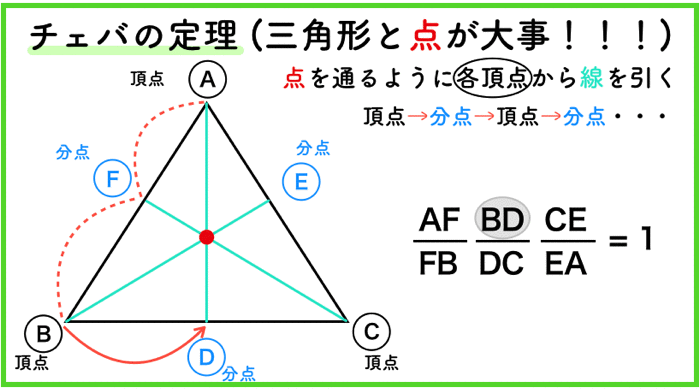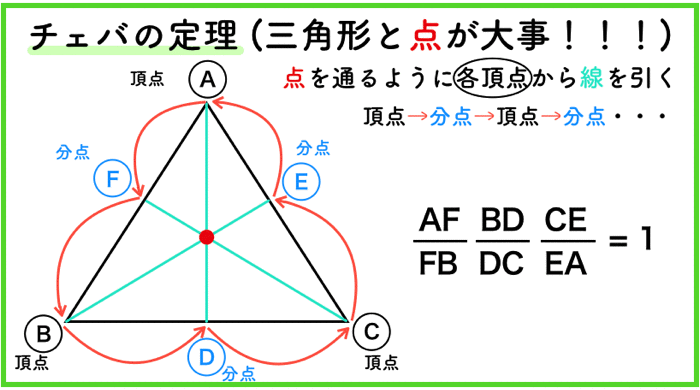



年 センター 数学1a チェバの定理 メネラウスの定理ってこんなに簡単だったんだ



チェバの定理とメネラウスの定理をてんびん算と連比で解く 父ちゃんが教えたるっ



0 件のコメント:
コメントを投稿